李群李代数

说到李群，就不得不提挪威数学家马里乌斯·索菲斯·李（Marius Sophus Lie），李群和李代数都是他创立的。

李群的诞生与伽瓦罗的群论一脉相承，1870年普法战争时期，Lie在巴黎用德语写的数学笔记被认为是间谍在传递加密信息，被捕关了一个月。获释后Lie就开始研究群论，Lie了解到伽罗瓦在40年前使用群论来解五次以五次以上多项式的解，Lie想使用同样的方法去找微分方程的对称性，再利用对称性简化求解微分方程，但是Lie发现用群的方法只能解决对称性离散的微分方程，而对于对称性连续变化的微分方程，并不能使用群的方法。但是，对称性连续变换的微分方程，既有群的结构，又有流形的结构，于是，李群诞生了。李群与生俱来的性质（连续对称），而连续对称是物理中很多系统（粒子相互作用、动量守恒、能量守恒等）的基本原则，因此，李群才在物理中有机会大显身手。再加上自然界中有不少连续对称性的系统（例如引力、电磁力等），李群在物理中的地位就更重要了。在1918年，埃米·诺特证明了李群也是一些最基本的物理学守恒定律的基础。她指出，对于任何可以用李群描述的物理系统对称性，都存在相应的守恒定律。

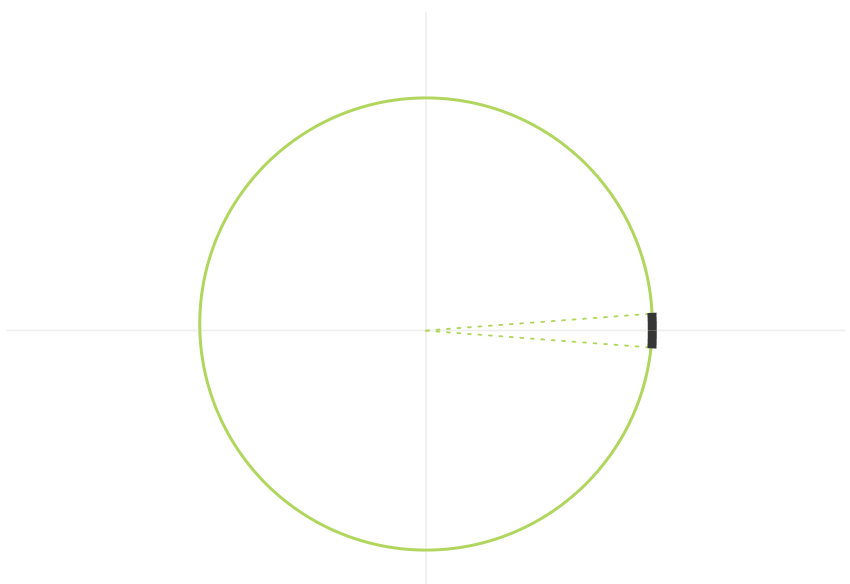
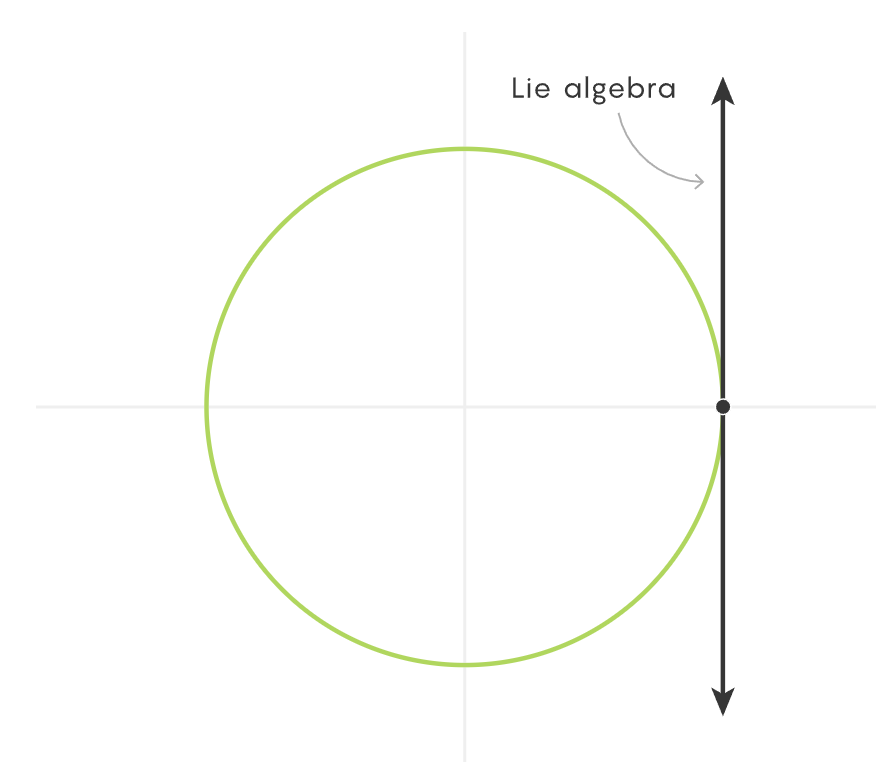
之前在另外一篇文章中看到过，作者用飞盘旋转（飞盘旋转 1.5 度、15 度还是 150 度，旋转任意实数，飞盘看起来都一样。与三角形不同，飞盘有无穷多个对称性），解释了什么是一个二维空间的特殊正交群（这些旋转构成一个名为SO(2)的群），同时也是最简单的非平凡李群，当飞盘旋转角度无限趋近于零时，飞盘的每一次旋转都可以用坐标平面上的一个点，可以在该点作一条切线来描述旋转，这条切线就叫做李代数。